AVL树的插入与删除

AVL树

简介

在计算机科学中，AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。

AVL树得名于它的发明者 G. M. Adelson-Velsky 和 Evgenii Landis，他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。

图例

• AVL树示例，如下图：

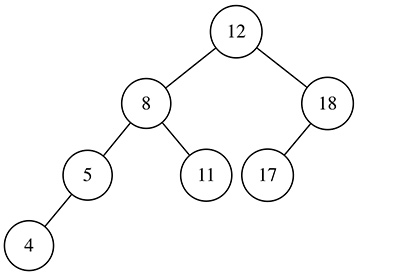
每个节点的左右子树高度差不大于1。

• 非 AVL树，如下图：

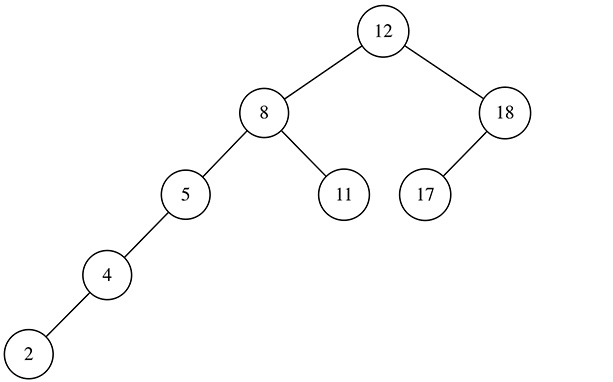
节点 5 的左右子树高度差大于 1。

意义

许多二叉搜索树的操作（例如：搜索、插入、删除、最大值、最小值等）需要 $O(h)$ 的时间复杂度，其中 $h$ 为树的高度。最差的情况遇到完全倾斜的树，时间复杂度会变为 $O(n)$ 。如果每次插入或删除节点后都能保证树的高度为 $O(\log{n})$ 的话，那就可以使得时间复杂度上限变为 $O(\log{n})$。使用 AVL树可以使树的高度保持为 $O(\log{n})$。

复杂度

算法	平均	最差
空间	$O(n)$	$O(n)$
搜索	$O(\log{n})$	$O(\log{n})$
插入	$O(\log{n})$	$O(\log{n})$
删除	$O(\log{n})$	$O(\log{n})$

树旋转

简介

在对二叉搜索树进行插入或删除操作后，可能会造成树的不平衡，所以需要对不平衡的节点进行旋转操作来保持平衡。

树旋转（英语：Tree rotation）是对二叉树的一种操作，不影响元素的顺序（二叉搜索树，但会改变树的结构。

一般有两种旋转方式：

• 左旋转，逆时针旋转
• 右旋转，顺时针旋转

如图所示：

旋转后仍可以保证 $T1 < x < T2 < y < T3$。

维基百科上的动画表达更加清晰：

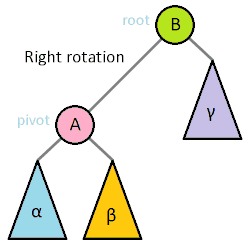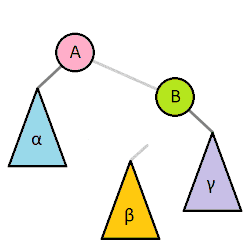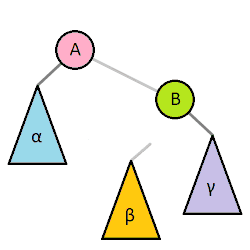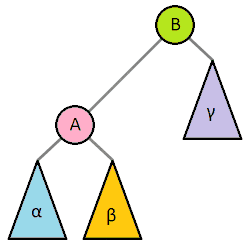
由Tar-Elessar - 自己的作品，CC BY-SA 4.0，https://commons.wikimedia.org/w/index.php?curid=34521454

需要进行旋转的情况

当执行完二叉搜索树的节点插入或删除后，有四种情况会出现树不平衡，需要进行旋转操作：

• 左左情况
• 左右情况
• 右右情况
• 右左情况

下面使用图片说明各种情况：

左左情况

节点 z 的左右子树高度差大于 1，处于不平衡状态。需要右旋转。

左右情况

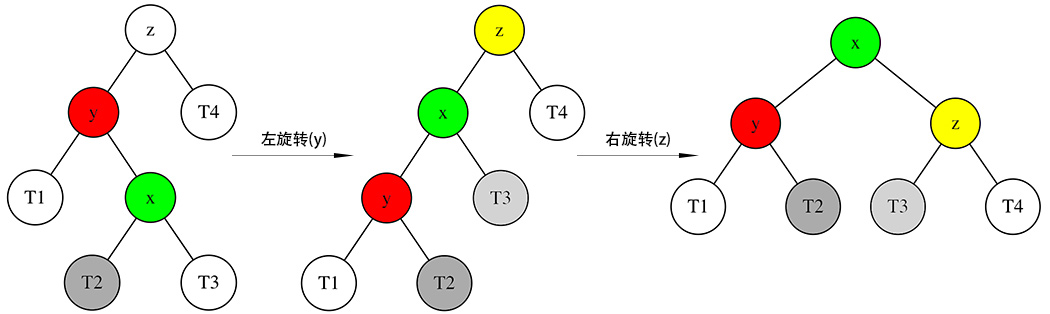
首先将节点 y 进行左旋转，变成左左情况，再进行右旋转。

右右情况

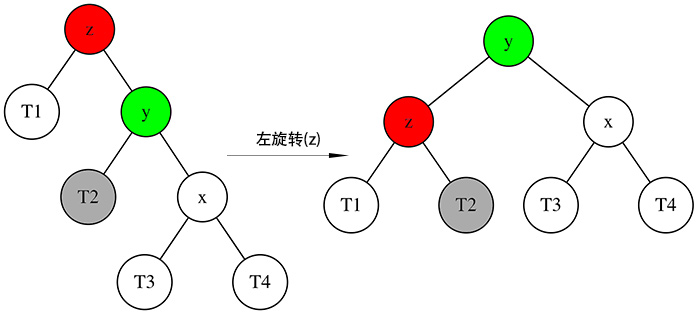
节点 z 的左右子树高度差大于 1，处于不平衡状态。需要左旋转。

右左情况

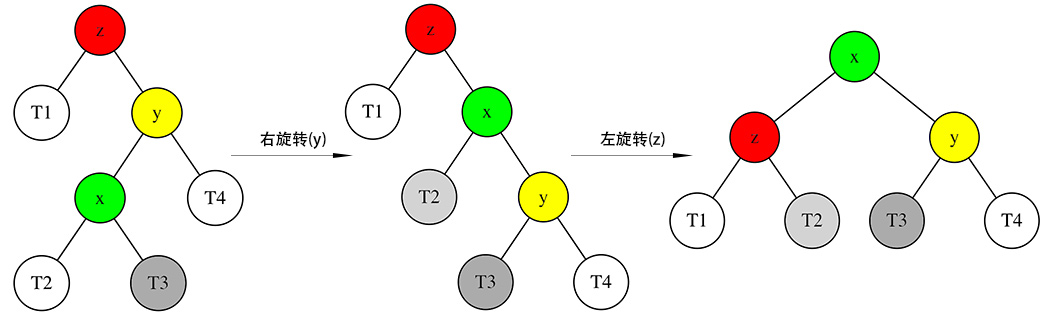
先将节点 y 进行右旋转，变成右右情况，再进行左旋转。

实现(JavaScript)

AVL树类

class AVLTreeNode {
  constructor(val) {
    this.val = val;
    this.left = null;
    this.right = null;
    this.height = 1;
  }
}

左旋转

/**
 * 节点左旋转
 *  x             y
 *   \           /
 *    y   -->   x
 *   /           \
 *  t2            t2
 * @param {AVLTreeNode} x 根节点
 * @returns {AVLTreeNode}
 */
function leftRotate(x) {
    const y = x.right;
    const t2 = y.left;

    // 执行旋转
    y.left = x;
    x.right = t2;

    // 更新节点高度
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;

    // 返回新的根节点
    return y;
}

右旋转

/**
 * 节点右旋转
 *    y          x
 *   /            \
 *  x      -->     y
 *   \            /
 *    t2         t2
 * @param {AVLTreeNode} y 根节点
 * @returns {AVLTreeNode}
 */
function rightRotate(y) {
    const x = y.left;
    const t2 = x.right;
    
    // 执行旋转
    x.right = y;
    y.left = t2;

    // 更新节点高度
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

    // 返回新的根节点
    return x;
}

插入节点

/**
 * 采用递归的方法将值插入树中，
 * 返回修改后的根节点。
 * @param {AVLTreeNode} node 
 * @param {number} val 
 * @returns {AVLTreeNode}
 */
function insert(root, val) {
    // 1. 执行普通的二叉搜索树节点插入
    if(!root) {
        return new AVLTreeNode(val);
    }
    if(val < root.val) {
        root.left = insert(root.left, val);
    } else if(val > root.val) {
        root.right = insert(root.right, val);
    } else {
        return root;
    }

    // 2. 更新根节点的高度
    root.height = 1 + Math.max(getHeight(root.left), getHeight(root.right));

    // 3. 返回平衡后的节点
    return balanceRoot(root);
}

删除节点

/**
 * 采用递归的方法来删除树中的值。
 * 返回修改后的根节点。
 * @param {AVLTreeNode} root 
 * @param {number} val 
 * @returns {AVLTreeNode}
 */
function deleteNode(root, val)  
{  
    // 1. 执行普通的二叉搜索树节点删除
    if (!root) {
        return root;
    }
  
    // val 小于根节点的值，查找左子树
    if ( val < root.val ) {
        root.left = deleteNode(root.left, val);  
  
    // val 大于根节点的值，查找右子树
    } else if( val > root.val ) {
        root.right = deleteNode(root.right, val);  

    // val 等于根节点的值，则此节点需要被删除
    } else {  
        // 只有一个子树或者没有子树
        if(!root.left || !root.right) {  
            let temp = root.left ? root.left : root.right;
  
            // 没有子树
            if (!temp) {  
                temp = root;  
                root = null;  
            } else { // 只有一个子树 
                root = temp; // 将 root 赋值为子树
            }
        } else {  
            // 左右子树同时存在
            // 找到中序遍历中根节点的下任节点，即右子树中值最小的节点 
            const temp = minValueNode(root.right);  
  
            // 使用这个节点来作为新的根节点
            root.val = temp.val;  
  
            // 删除右子树中值最小的节点
            root.right = deleteNode(root.right, temp.val);  
        }  
    }  
  
    // 没有子树
    if (!root) {
        return root;  
    }
  
    // 2. 更新根节点的高度
    root.height = 1 + max(getHeight(root.left), getHeight(root.right));  
  
    // 3. 返回平衡后的节点
    return balanceRoot(root);
}

平衡处理

/**
 * 返回平衡后的根节点
 * @param {AVLTreeNode} root
 * @returns {AVLTreeNode}
 */
function balanceRoot(root) {
    // 获取根节点的平衡因子，来判断是否保持平衡状态
    const balance = getBalance(root);

    // 如果节点不平衡，有四种情况

    // 左左情况
    if(balance > 1 && val < root.left.val) {
        return rightRotate(root);
    }

    // 右右情况
    if(balance < -1 && val > root.right.val) {
        return leftRotate(root);
    }

    // 左右情况
    if(balance > 1 && val > root.left.val) {
        root.left = leftRotate(root.left);
        return rightRotate(root);
    }

    // 右左情况
    if(balance < -1 && val < root.right.val) {
        root.right = rightRotate(root.right);
        return leftRotate(root);
    }

    // 依然保持平衡，不做处理，返回根节点
    return root;
}

辅助函数

/**
 * 获取节点高度
 * @param {AVLTreeNode} n 
 * @returns {number}
 */
function getHeight(n) {
    if(!n) {
        return 0;
    }
    return n.height;
}

/**
 * 获取节点平衡因子，左右子树高度差
 * @param {AVLTreeNode} n 
 * @returns {boolean}
 */
function getBalance(n) {
    if(!n) { return 0; }
    return getHeight(n.left) - getHeight(n.right);
}

/**
 * 给定一个非空二叉搜索树，找出最小值的节点。
 * 注意：无需遍历整个树。
 * @param {AVLTreeNode} node 
 * @returns {AVLTreeNode}
 */
function minValueNode(node) {
    let p = node;
    while(p.left) {
        p = p.left;
    }
    return p;
}

复杂度分析

• 左右旋转操作：$O(1)$，因为只操作了节点指针。
• 更新节点高度和获取平衡因子：$O(1)$。
• 插入节点：$O(h)$ ，$h$ 为树的高度。因为 AVL 树是平衡二叉树，高度为 $h = \log{n}$，所以复杂度为 $O(\log{n})$。
• 删除节点：同插入节点为 $O(h)$。

参考链接

• AVL Tree | Set 1 (Insertion), GeeksforGeeks.
• AVL Tree | Set 2 (Deletion), GeeksforGeeks.
• AVL数, Wikipedia.
• 树旋转, Wikipedia.